Difference between revisions of "Cellular automation"
Caseorganic (Talk | contribs) |
Caseorganic (Talk | contribs) |
||
| Line 11: | Line 11: | ||
[[Image:conways-game-of-life.png|380px|thumb|right|"One iteration in Conway's game of life. Little animals (1) die from loneliness. Little animal (2) dies from overspill population. Little animal (3) survives. Little animals (4) are procreated". <ref>[http://www.leda-tutorial.org/en/official/ch02s02s02.html LEDA Tutorial - 2.2.2. Two-dimensional arrays]</ref>]] | [[Image:conways-game-of-life.png|380px|thumb|right|"One iteration in Conway's game of life. Little animals (1) die from loneliness. Little animal (2) dies from overspill population. Little animal (3) survives. Little animals (4) are procreated". <ref>[http://www.leda-tutorial.org/en/official/ch02s02s02.html LEDA Tutorial - 2.2.2. Two-dimensional arrays]</ref>]] | ||
| − | The | + | The "game became widely known when it was mentioned in an article published by Scientific American in 1970".<ref>[http://www.bitstorm.org/gameoflife/ Bitstorm.org Game of Life]</ref><ref>[http://ddi.cs.uni-potsdam.de/HyFISCH/Produzieren/lis_projekt/proj_gamelife/ConwayScientificAmerican.htm Mathematical Games: The fantastic combinations of John Conway's new solitaire game "life"] by Martin Gardner. Scientific American 223 (October 1970): 120-123.</ref> |
| − | + | In Conway's [[Game of Life]], "life has only two states, 1 and 0, standing for "living" and "dead", respectively. The transition rule is also simple. You look at all eight cells immediately around you. If less than two of your neighbors are alive, you die. If exactly two of your neighbors are live, you don't change. If exactly three of your neighbors are alive, you will be alive next turn, regardless of your current state. If four or more of your neighbors are alive, you are over-crowded and you die". <ref>http://cscs.umich.edu/~crshalizi/notabene/cellular-automata.html</ref> | |
| − | + | ||
| − | + | ||
"It turns out that the number of interesting configurations you can make from these elements is immense: things which blink and oscillate; things which glide across the plane; things which eat the gliders; things which throw off the gliders like waste". <ref>http://cscs.umich.edu/~crshalizi/notabene/cellular-automata.html</ref> | "It turns out that the number of interesting configurations you can make from these elements is immense: things which blink and oscillate; things which glide across the plane; things which eat the gliders; things which throw off the gliders like waste". <ref>http://cscs.umich.edu/~crshalizi/notabene/cellular-automata.html</ref> | ||
Revision as of 19:31, 14 February 2011
Definition
"Cellular automata are the simplest models of spatially distributed processes. They consist of an array of cells, each of which is allowed to be in one of a few states. At the same time, each cell looks to its neighbors to see what states they are in. Using this information each cell applies a simple rule to determine what state it should change to. This basic step is repeated over the whole array, again and again".[1]
"A one-dimensional cellular automaton consists of two things: a row of "cells" and a set of "rules"...[2] "Each of the cells can be in one of several "states". The number of possible states depends on the automaton. Think of the states as colors. In a two-state automaton, each of the cells can be either black or white. Of course, you might just as easily use purple and orange to represent the states, if you thing that's prettier. In a three-state automaton, the states might be black, red, and blue". [3]
"A CA doesn't just sit there. Over time, the cells can change from state to state. The cellular automaton's rules determine how the states change. It works like this: When the time comes for the cells to change state, each cell looks around and gathers information on its neighbors' states. (Exactly which cells are considered"neighbors" is also something that depends on the paticular CA.) Based on its own state, its neighbors' states, and the rules of the CA, the cell decides what its new state should be. All the cells change state at the same time. You should think of the row of cells as a miniature "world" that runs through a sequence of "years" or "generations." At the end of each year, all the cells simultaneously decide on their state for the next year". [4]
Conway's Game of Life
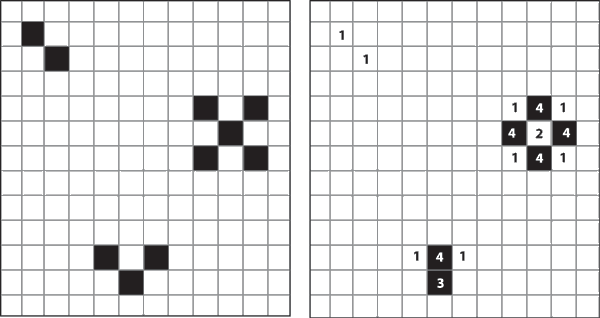
The "game became widely known when it was mentioned in an article published by Scientific American in 1970".[6][7]
In Conway's Game of Life, "life has only two states, 1 and 0, standing for "living" and "dead", respectively. The transition rule is also simple. You look at all eight cells immediately around you. If less than two of your neighbors are alive, you die. If exactly two of your neighbors are live, you don't change. If exactly three of your neighbors are alive, you will be alive next turn, regardless of your current state. If four or more of your neighbors are alive, you are over-crowded and you die". [8]
"It turns out that the number of interesting configurations you can make from these elements is immense: things which blink and oscillate; things which glide across the plane; things which eat the gliders; things which throw off the gliders like waste". [9]
Related Articles
References
- ↑ http://www.exploratorium.edu/complexity/CompLexicon/automaton.html
- ↑ http://math.hws.edu/xJava/CA/CA.html
- ↑ http://math.hws.edu/xJava/CA/CA.html
- ↑ http://math.hws.edu/xJava/CA/CA.html
- ↑ LEDA Tutorial - 2.2.2. Two-dimensional arrays
- ↑ Bitstorm.org Game of Life
- ↑ Mathematical Games: The fantastic combinations of John Conway's new solitaire game "life" by Martin Gardner. Scientific American 223 (October 1970): 120-123.
- ↑ http://cscs.umich.edu/~crshalizi/notabene/cellular-automata.html
- ↑ http://cscs.umich.edu/~crshalizi/notabene/cellular-automata.html